티스토리 뷰
목차

정수
정수는 모든 정수 및 음수를 포함하며 분수 또는 소수 부분은 없는 숫자 집합입니다.
이에는 양의 정수, 음의 정수, 그리고 0이 포함됩니다.
정수의 특징:
전체 수: 정수는 0, 양의 전체 수(자연수), 그리고 음의 전체 수를 포함합니다.
기호: 모든 정수의 집합은 𝑍로 표시됩니다.
이는 독일어 "Zahlen"(숫자를 의미)에서 유래되었습니다.
분수/소수 없음: 정수에는 분수나 소수가 포함되어 있지 않습니다.
정수의 예시: 1, 2, 3 … 1,2,3,…은 양의 정수입니다.
−1, −2, −3, … −1,−2,−3,…은 음의 정수입니다.
0도 정수로 간주되며, 양수도 음수도 아닙니다.
정수는 물체를 세거나, 온도 변화를 표현하거나, 은행 거래(예금 및 출금) 등 실생활 다양한 맥락에서 사용됩니다.
정수와 유리수 - 정수란 무엇일까?
소수
소수는 소수점을 포함하는 숫자입니다. 소수점은 숫자의 정수 부분과 분수 부분을 분리합니다. 소수는 그 특성에 따라 유한소수와 무한소수로 구분 할 수 있습니다.
소수의 특징:
소수점: 소수의 주요 특징은 소수점의 존재입니다.
부분: 소수에는 두 부분이 있습니다: 소수점 이전의 부분은 전체 수 부분을 나타내고, 소수점 이후의 부분은 분수 부분을 나타냅니다.

유리수와 무리수
유한 소수와 무한 소수: 소수는 유한소수(예: 0.75), 반복무한소수(예: 0.333333 …), 또는 비반복무한소수 (예: 𝜋, e, √2, √3) 가 있습니다.
소수의 예시:
유한 소수: 12.34 / 12.34에서 "12"는 전체 수 부분이고, "34"는 분수 부분입니다.
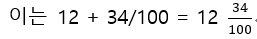
유리수 입니다.

은 유리수 입니다.
비반복 무한 소수: √2 의 소수 확장은 대략 1.414213562... 로 무리수 입니다.
소수는 금융, 과학, 일상 생활 등에서 보다 정확한 측정과 계산에 매우 유용합니다.
정수와 소수는 함께 다양한 수를 포괄하며 다양한 수학적 및 실용적 응용 프로그램에 필수적입니다. 이들은 다양한 정밀도로 계산을 수행하고 실제 상황에서 넓은 범위의 값을 나타낼 수 있도록 도와줍니다.
블로그에는 분수, 지수, 제곱근 등을 표현할 수 없으므로 2 / 3 , 2 ^ 3 , √3 과 같이 표현 할 것 이기 때문 입니다.
강의록을 올리지 못한 이유가 msworld, 한글에서 수식을 만들 수는 있지만 블로그에서는 표현이 되지 않습니다. 착오 없으시기 바랍니다.
다음시간에는 소수를 분수로 변환하는 방법에 대하여 알아보겠습니다. 오늘은 여기까지..
무리수의 예


'중학수학' 카테고리의 다른 글
| 꼬리에 꼬리를 무는 수학 (46) | 2024.05.18 |
|---|---|
| 수학은 왜 어렵지 (2) | 2024.05.18 |
| 중1 수학 - 2강 지수, 약수, 배수, 소인수 분해 (42) | 2024.05.10 |
| 중2 수학 - 1강 유리수 (2) | 2024.05.06 |
| 중1 수학 - 1강 소수와 합성수 (2) | 2024.05.06 |
